Desfaziendo Entuertos

Geometría 2D (I): la circunferencia.

16 septiembre, 2011 20:46

Definición.

Circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. La distancia constante de un punto cualquiera ‘P’ al centro se llama radio.

Ecuación

Sea un sistema de referencia ortonormal $(O, \vec{i}, \vec{j})$ .

Sea ‘C’ (a, b) el centro de la circunferencia de radio ‘r’.

Sea ‘P’ (x, y) un punto genérico de ella.

La ecuación geométrica es:

$d(C, P)=\sqrt{(x-a)^2+(y-a)^2}=r$ .

$(x-a)^2+(y-a)^2=r^2$ .

Área del círculo

Sea la circunferencia con centro en el origen de referencia $(x)^2+(y)^2=r^2$ .

De donde:

$y=\sqrt{r^2-x^2}$ .

Por simetría:

$S=4\int_0^{r}y \: dx=4\int_0^{r}\sqrt{r^2-x^2} \: dx$ .

Hacemos el siguiente cambio de variable:

$x=\sin{(t)}$ .

$dx=r\cos{(t)}dt$ .

$Para \: x=0 \: \: tenemos \: t=0$ .

$Para \: x=r \: \: tenemos \: t=\displaystyle\frac{\pi}{2}$ .

Sustituyendo:

$S=4\int_0^{r}\sqrt{r^2-x^2} \: dx=4\int_0^{\frac{\pi}{2}}\sqrt{r^2-r^2\sin^2{(t)}} \:r\cos{(t)}\: dt$ .

$S=4 \:r^2\int_0^{\frac{\pi}{2}}\sqrt{1-\sin^2{(t)}} \:\cos{(t)}\: dt$ .

Sabemos que:

$\cos^2(t)+\sin^2(t)=1$ .

$\cos^2(t)=1-\sin^2(t)$ .

$\cos(t)=\sqrt{1-\sin^2(t)}$ .

Sustiuyendo en nuestra ecuación:

$S=4 \:r^2\int_0^{\frac{\pi}{2}}\cos(t) \:\cos{(t)}\: dt=4 \:r^2\int_0^{\frac{\pi}{2}} \:\cos^2{(t)}\: dt$ .

Utilizando las razones trigonométricas del angulo doble:

$\cos(2t)=\cos^2(t)-\sin^2(t)=\cos^2(t)+\cos^2(t)-1=2\cos^2(t)-1$ .

$\cos^2(t)=\displaystyle\frac{1+\cos(2t)}{2}$ .

Obtenemos:

$S=4 \:r^2\int_0^{\frac{\pi}{2}} \:\cos^2{(t)}\: dt=4 \:r^2\int_0^{\frac{\pi}{2}} \:\frac{1+\cos{(2t)}}{2}\: dt$ .

$S=2{r^2}\left[t-\displaystyle\frac{\sin(2t)}{2}\right]_0^{\pi/2}$ .

$S=2{r^2}\left[\displaystyle\frac{\pi}{2}-\displaystyle\frac{\sin(\pi)}{2}-0+\displaystyle\frac{\sin(0)}{2}\right]=\pi{r^2}$ .

Longitud de la circunferencia

Por simetría:

$S=4\int_0^{r} \sqrt{1+(y\:')^2} \: dx$ .

Hallamos la deriva al cuadrado de nuestra función:

$y=\sqrt{r^2-x^2}$ .

$y\:'=\displaystyle\frac{-x}{\sqrt{r^2-x^2}}$ .

$(y\:')^2=\displaystyle\frac{x^2}{{r^2-x^2}}$ .

Sustituyendo:

$S=4\int_0^{r} \sqrt{1+(y\:')^2} \: dx=4\int_0^{r} \sqrt{1+\displaystyle\frac{x^2}{{r^2-x^2}}} \: dx=4r\int_0^{r}\displaystyle\frac{1}{\sqrt{r^2-x^2} \: dx}$ .

$S=4r\left[\arcsin{\displaystyle\frac{x}{r}}\right]_0^r=2 \: \pi \: r$ .

Longitud arco circunferencia

$L=2 \pi r \displaystyle\frac{\theta}{2 \pi}=r \theta$ .

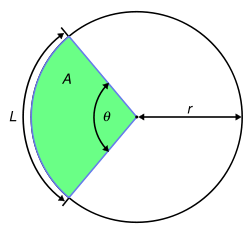
Área sector circular

$A=\pi r^2 \displaystyle\frac{\theta}{2 \pi}=\displaystyle\frac{r^2 \theta}{2}$ .

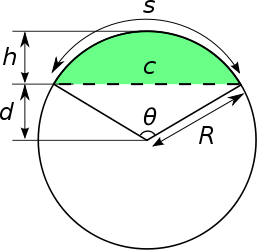
Área del segmento circular

$A=\pi R^2\displaystyle\frac{\theta}{2 \pi}-\displaystyle\frac{R^2 \sin{\theta}}{2}$ .

$A=\displaystyle\frac{R^2}{2}(\theta-\sin{\theta})$ .

Escrito por: Crosmen

Categorías: Geometría, Matemáticas

Etiquetas: circunferencia, geometria

« Older Newer »

Una respuesta to “Geometría 2D (I): la circunferencia.”

I simply want to tell you that I am just very new to weblog and honestly savored your web page. Most likely I’m planning to bookmark your site . You definitely have remarkable articles and reviews. Many thanks for sharing with us your webpage.

By Jerrie Jakob on 15 octubre, 2011 a 16:38

Deja una respuesta

Mobile Site | Full Site

Get a free blog at WordPress.com Theme: WordPress Mobile Edition by Alex King.

Desfaziendo Entuertos

Geometría 2D (I): la circunferencia.

Tu voto:

Comparte esto:

Relacionado

Una respuesta to “Geometría 2D (I): la circunferencia.”

Deja una respuesta